Few months back I blogged about
difference between explicit dynamic and implicit analysis. Concisely
summarizing, an implicit analysis is the one which is independent of time and
explicit is the one which is of a short duration and time dependent. In
this post, I would be going into details regarding an Implicit Finite Element
Analysis. Newton-Raphson (NR) method is the commonly used method for most of
the implicit FE solvers. In simple numerical terms, the N-R method is used for
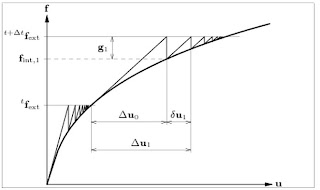
finding successively better approximations. Figure 1 shows the general
iterative process for an implicit analysis. Click here to
read more about N-R method.
Figure
1: General Iterative
process for Implicit Analysis
The Regular and
the Modified method are two variants of Newton-Raphson
method. Both of them iteratively increment the displacement vector. The
equation (1) is used by both the methods to determine the increments.
Where Ki is the stiffness matrix
which represents the tangential stiffness of the structure, 'u' is the
displacement and 'g' is the out of balance force. The evaluation of stiffness relation in equation (1) forms a
basis for differentiation between Regular and Modified NR method.
Ki =
equation (1)
Regular Newton-Raphson method: In the Regular Newton-Raphson iteration, the
stiffness relation (equation 1) is evaluated every iteration as shown in Figure
2. This means that the prediction of change in displacements is based on
the last known or predicted situation which necessarily need not be an
equilibrium state.
The Regular and
the Modified method are two variants of Newton-Raphson
method. Both of them iteratively increment the displacement vector. The
equation (1) is used by both the methods to determine the increments.
Where Ki is the stiffness matrix
which represents the tangential stiffness of the structure, 'u' is the
displacement and 'g' is the out of balance force. The evaluation of stiffness relation in equation (1) forms a
basis for differentiation between Regular and Modified NR method.
| Ki = |
equation (1)
This method brings
convergence within only a few iterations. However the main disadvantages
of the method include time consumption and accuracy of the solution. As the
stiffness matrix has to be setup for every iteration, using a direct solver can
result into heavy computational costs as a consequence of decomposition of the
matrix. The accuracy of the solution would depend on the initial
prediction or guess, if it is far from the final solution, the method easily
fails because of divergence. Thus, the regular method requires fewer iterations
but is relatively time consuming.
Modified Newton-Raphson
method: The Modified Newton-Raphson method only evaluates the stiffness relation (equation 1) at the
start of the increment as shown in figure 3. The prediction is always
based on a converged equilibrium state as opposed to that of the regular
method. This method converges slower than the regular method, however, for
every iteration setting up of a new stiffness matrix is not required. Generally
speaking, the modified method would require larger number of iterations but
each of the iterations take less time as compared to the regular method.
The Modified Newton-Raphson
process can sometimes converge in situations where the regular method would
not. For more reading, kindly refer to the links below:
Kindly ignore the formatting, blogger editor gave me a hard time. Time to switch to wordpress.
Note: Most of the material has
been referred from the TNO Diana manual. I do not claim any copyrights. If you are interested in improving the content, kindly let me know, I can grant you access to the post.




No comments:
Post a Comment